hitcon2018-lost-modulus

26 Dec 2018

Reading time ~3 minutes

Lost modulus

0x01 前情提要

惯例题目放最后

这道题在ctftime上找到三个WP

Pham Solo 2的，hellman的和P4的。

P4的WP说它是a textbook implementation of Paillier cryptosystem

~~……我还以为是教科书式的RSA，好像是看了Lost Key的WP串台了~~

Paillier加密是什么，为什么不问问神奇的维基百科呢

简单描述一下，

它的加密为：

def encrypt(g,n,data):
  num = bytes_to_long(data)
  #将消息转化为数字
  res = pow(g,num,n*n)
  #g的m次方 mod n的平方
  r = rnd.randint(0,n-1)
  #随机选择一个r，sit： 0 <= r <= n-1
  magic = pow(r,n,n*n)
  #r的n次方 mod n的平方
  res = (res*magic)%(n*n)
  #即g的m次方 乘 r的n次方 mod n的平方
  return long_to_bytes(res).encode('hex')
  #数字转十六进制字符

也就是密文c = g**m * r**n mod n**2 其中n和g是公钥，m是信息，r是一个随意选择的，小于N的，和N互素的数

解密：

def decrypt(phi,n,u,data):
  num = bytes_to_long(data)
  res = pow(num,phi,n*n)
  #c的phi次方 mod n的平方
  res = (res - 1)/n
  res = (res*u)%n
  return long_to_bytes(res).encode('hex')

是的我都照搬题目的源码 :D 解密：m = [(((c**phi mod n**2) -1) / n ) * u] mod n

没错加密时mod n的平方，而解密是mod n

注意这里的加解密可能和《基于同态加密系统的图像鲁棒可逆水印算法》里对Paillier加密系统的介绍对不上，这是因为维基百科里有提到的：

If using p,q of equivalent length, a simpler variant of the above key generation steps would be to set ,andwhere

所以我们会看到题目里的加密是：（Pham Solo 2 WP里的公式）

而这篇论文里的是：

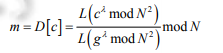
好的加解密描述完毕，再看看题目还写了什么。

首先是秘钥生成

  p = getPrime(512)
  q = getPrime(512)
  n = p*q
  phi = (p-1)*(q-1)
  g = n+1
  u = invert(phi,n)

p和q是两个大素数，n是p和q的成绩，phi是n的欧拉函数，在这里是(p-1)*(q-1)，然后g是n+1，u是n 在 mod n 下模反元素

然后它把flag加密（print encrypt(g,n,flag)）之后print给了我们

  for i in xrange(2048):
    m = raw_input('cmd: ')
    if m[0] == 'A':
      m = raw_input('input: ')
      try:
        m = m.decode('hex')
        print encrypt(g,n,m)
      except:
        print 'no'
        exit(0)
    if m[0] == 'B':
      m = raw_input('input: ')
      try:
        m = m.decode('hex')
        print decrypt(phi,n,u,m)[-2:]
      except:
        print 'no'
        exit(0)

之后给我们提供了2048次交互，每次交互我们有两种选择——

选择A会加密我们发送的信息，并把密文print给我们：

   if m[0] == 'A':
      m = raw_input('input: ')
      try:
        m = m.decode('hex')
        print encrypt(g,n,m)

选择B会解密我们发送的信息，但只会把明文最后的两个字符print给我们

    if m[0] == 'B':
      m = raw_input('input: ')
      try:
        m = m.decode('hex')
        print decrypt(phi,n,u,m)[-2:]

0x02 第一步：恢复公钥

解法我先按着P4说的来。

如果我们发送给它加密的数字大于n然后再解密它，他就会被mod n cut掉一部分，这样可以慢慢地恢复n的所有比特……

这里我看的时候蠢到有点绕进去了，注意加密算法本来就要求，解密的是要mod n的。

犯蠢的时候看看ctfwikiRSA parity oracle有利于清醒（×

也就是，发送x > n，return x-n；发送 x < n，return x

然后还有一点，n是大素数p和q的乘机，p和q是奇数，n也是奇数

所以我们发送 x = 2的y次方，就1后面很多个0那种，如果解密后返回的是”00”，显然就是返回了x，则说明x小于n；而如果不是，因为 x-n，偶数减奇数是奇数，所以不会返回”00”，此时我们发送的x就大于n。

这样就能慢慢把n的高比特位弄出来。

最后剩下8个bit，因为解密后会返回一个字符，也就是8bit的信息，所以我们可以根据返回结果遍历所有可能性，如果x%n的最后八位和返回的结果一致，就得到了正确的n。

即，当我们确定了前127个字符后，将最后的1个字符取0xff，拼成x发送给服务器进行加密再解密，这样会返回x%n的最后8位，我们遍历2**8=256个可能性，找到%n==返回结果的确定的x就可以了。

以上，我们就成功知道了模数n。

0x03 第二步：get flag 的后7个字符

我们可以很简单地利用Paillier的同态性一个一个比特地把flag还原出来。把加密了的flag传送给服务器进行解密，我们就能得到flag的最后一个字节了，现在我们想要做的是从最后一个字节开始，一个字节一个字节地将flag从后往前还原。也就是说，如果我们的密文解密被解密成了alamakota，我们想要找到一个有相同结果的密文。这样做是可以的，只要我们先把最后一个字节替换成\x00，然后我们除以256来让它变成alamakot就行了……

根据维基百科，Paillier的同态性让我们有以下等式：

所以

当我们通过服务器的解密得到flag的最后一个字符之后，

因为

密文m1乘密文m2再解密，等于m1+m2

令m2为\x00，将flag的密文乘上256的模反元素，其实就是flag除256bits的结果，再进行解密，就能得到 m1-m2 = flag - flag[-1] =flag[0:-1]，就得到了flag的倒数第二个字符（因为解密只返回最后一个字符），以此类推，我们将会得到flag的最后14个明文。

        last_byte = dec(long_to_bytes(flag)).decode("hex")
        f += last_byte
        print(f[::-1])
        sub = paillier_encrypt_simple(n - bytes_to_long(last_byte), g, n)
        flag = flag * sub % (n * n)
        flag = pow(flag, divisor, n * n)

在p4的代码里，

flag是被加密了的flag密文，假设为m1

f是存储破译出来的flag的后面的字节的明文的

sub是E(-last_byte)，假设为m2

所以flag* sub % (n * n)就是flag（再次提醒，这里的flag是flag的密文）和(-last_byte)的密文相乘

记得我们有（以下内容为超简化版描述）：

D( E(m1) * E(m2) ) = m1 + m2

D( E(m1) * E(-m2) ) = m1 - m2

所以，flag = flag * sub % (n * n)可以理解为E(m1) * E(-m2)

以上我们就能把alamakota转化为alamakot\x00了

然后维基百科还告诉我们一条式子

所以代码的最后一行pow(flag, divisor, n * n)是除以256，就是把alamakot\x00转化为alamakot

所以这套操作其实是干了这样的事：

>>> a = "alamakot"
>>> b = 't'
>>> #flag = flag * sub % (n * n)
>>> c = int(a.encode('hex'),16) - int(b.encode('hex'),16)
>>> hex(c)[2:-1].decode('hex')
'alamako\x00'
>>> #pow(flag, divisor, n * n)
>>> d = c/256
>>> hex(d)[2:-1].decode('hex')
'alamako'

这样就能将加密成“abcdefg”的密文，转化为加密成“abcdef”的密文了

又因为题目允许我们每次得到一个明文，因此我们就能依次从后往前逐个得出明文。

所以，请问神奇的海螺，为什么要先减去最后一个字符呢？为什么不能直接除256呢？

总之，这之后我们能得到flag的最后14个字符

0x04 第三步：get flag

因为flag比14字节长，所以我们要多次运行脚本，而每次运行脚本都要把已知的flag的后缀删掉。

源题目

#!/usr/bin/env python
from Crypto.Util.number import *
from gmpy import *
from random import *
import sys,os


sys.stdin  = os.fdopen(sys.stdin.fileno(), 'r', 0)
sys.stdout = os.fdopen(sys.stdout.fileno(), 'w', 0)
rnd = SystemRandom()

def encrypt(g,n,data):
  num = bytes_to_long(data)
  res = pow(g,num,n*n)
  r = rnd.randint(0,n-1)
  magic = pow(r,n,n*n)
  res = (res*magic)%(n*n)
  return long_to_bytes(res).encode('hex')

def decrypt(phi,n,u,data):
  num = bytes_to_long(data)
  res = pow(num,phi,n*n)
  res = (res - 1)/n
  res = (res*u)%n
  return long_to_bytes(res).encode('hex')

if __name__ == '__main__':
  p = getPrime(512)
  q = getPrime(512)
  n = p*q
  phi = (p-1)*(q-1)
  g = n+1
  u = invert(phi,n)
  flag = open('flag').read()
  print 'Here is the flag!'
  print encrypt(g,n,flag)
  for i in xrange(2048):
    m = raw_input('cmd: ')
    if m[0] == 'A':
      m = raw_input('input: ')
      try:
        m = m.decode('hex')
        print encrypt(g,n,m)
      except:
        print 'no'
        exit(0)
    if m[0] == 'B':
      m = raw_input('input: ')
      try:
        m = m.decode('hex')
        print decrypt(phi,n,u,m)[-2:]
      except:
        print 'no'
        exit(0)

Crypto